86. Electric field energy

According to the concepts of proximity theory all energy of charged bodies is concentrated in the electric field created by these bodies. Therefore, energy can be expressed through the strength of the electric field.

Let's define the energy of the electric field depending on its strength \(\overrightarrow{E}\,\) for a particular case of a plate capacitor filled with a substance with dielectric permittivity \(\varepsilon\). The energy of the capacitor can be calculated by finding the work that the electrostatic field forces will do when the plates move closer together.

Let the plates with area \(A\,\) be at a distance \(d\,\) from each other at the beginning (fig. 1, a). Let us denote the field strength inside the condenser \(E\). This strength is created by charges on both plates.

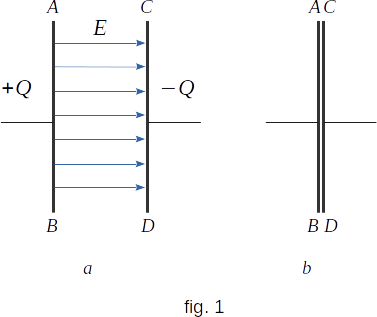
In order to calculate the field work, it is necessary to know the force acting from one plate to another. The field strength created by one of the plates is \(\frac{E}{2}\) (see section 84).

At \(Q\,=\,const ~\) the field strength of the plates remains constant, regardless of the position of the second plate relative to the first one.

Consequently, if the \(CD\,\) plate is shifted by distance \(d\,\) in the field of \(AB\,\) plate, positive Work will be done

\( W \,= \,\frac{Q\,E\,d}{2} \)

As in the uniform field

\( E\,d \,= \,V_1 \,- \,V_2 \)

where \(V_1 \,- \,V_2\) is the potential difference between the plates at the initial moment, then

\( W \,= \,\frac{Q(V_1 \,- \,V_2)}{2} \)

The work of internal forces in the system is equal to the change of potential energy \(U_c\), taken with inverse sign

\( \Delta{U_c} \,= \,U_2 \,- \,U_1 \,= \,-W \,= \,-\frac{Q(V_1 \,- \,V_2)}{2} \) (8-31)

But the energy \(U_2\) in the final state, when the plates come close and their charges \(+Q\) and \(-Q\) are neutralized (fig. 1, b), is equal to zero. Therefore, from equation \((8-31)\) we get the following equation for capacitor energy

\( U_c \,= \,U_1 \,= \,\frac{Q(V_1 \,- \,V_2)}{2} \) (8-32)

Using the capacitance definition \((8-29)\), this energy can be written in another form

\( U_c \,= \,\frac{Q^2}{2C} \,= \,\frac{C(\Delta{V})^2}{2} \)

where

\( \Delta{V} \,= \,V_1 \,- \,V_2 \)

Let's replace \(Q\) and \(V_1 \,- \,V_2\) with their values in equation \((8-32)\),

where \(A\,\) is the plate area, \(d\,\) is the distance between the plates and sigma \(\sigma\,\) is the surface charge density. Then

\( U_c \,= \,\frac{Q(V_1 \,- \,V_2)}{2} \,= \,\frac{\sigma\,\,A\,E\,d}{2}\)

In SI units the capacitor field is determined by equation

Therefore, the energy of a plate capacitor can be written in the following way

\( U_c \,= \,\frac{A\,d\,E}{2}\sigma \,= \,\frac{\varepsilon{_0}\varepsilon\,E^{2}\,A\,d}{2}\) (8-33)

By dividing \((8-33)\) by the volume \((Ad)\) occupied by the field, we obtain the energy per unit of volume, i.e. the density of energy

\( \eta_e \,= \,\frac{energy}{volume} \,= \,\frac{1}{2}\varepsilon{_0}\varepsilon\,E^{2}\) (8-34)

The most remarkable thing about the density of energy equation is that there are no traces of that particular example ( a plate capacitor ) that we considered. As always in physics, this means that the resulting equation \((8-34)\) is true not only for the uniform field of a plate capacitor, but in any other case. Moreover, the resulting equation for density energy is also true for electric fields that change with time.