78. Connection between electric field strength and potential difference

Between the electric field strength and the potential difference, there is an unambiguous relationship. The work on the displacement of the positive charge \(q\) when it is shifted to a small segment \(\Delta{\overrightarrow{l}}\) (fig. 1) is equal to

\( q\,E\,\Delta{l}\,\cos\alpha \,= \,q\,E_l\,\Delta{l} \)

where \(\alpha\) is the angle between \(\overrightarrow{E}\) and \(\Delta{\overrightarrow{l}}\), a \(E_l\) is the projection of vector \(\overrightarrow{E}\) to the direction \(\Delta{\overrightarrow{l}}\).
On the other hand, by definition of the potential difference \((8-23)\), the ratio of this work to charge \(q\) is equal (with the opposite sign) to the potential difference \(\Delta{V}\) at the ends of segment \(\Delta{\overrightarrow{l}}\).

\( E_l\,\Delta{l} \,= \,-\Delta{V} \) (8-25)

Therefore, knowing the field strength in each point, we can calculate the difference, potentials between any points. And knowing the difference of potentials between any points as close as possible, connected with the motion vector \(\Delta{\overrightarrow{l}}\), we can find the projection of field strength in the direction \(\Delta{\overrightarrow{l}}\)

\( E_l \,= \,\frac{\Delta{V}}{\Delta{l}} \)

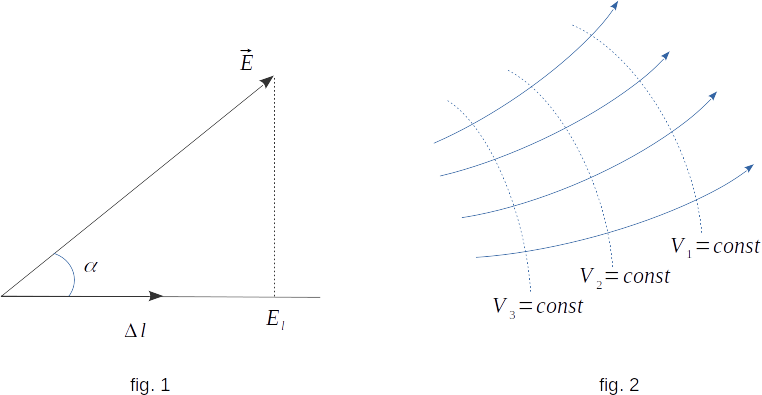
Equipotential surfaces.

Distribution of electric field in space can be qualitatively characterized not only by power lines, but also by surfaces of equal potential - equipotential surfaces.

The property of equipotential surfaces is that they are perpendicular to the power lines (fig. 2). Work the moving charge along the equipotential surface according to potential difference is zero, which means that the force acting on the charge is perpendicular to its movement.

The equipotential surface is, for example, the conductor surface in the equilibrium of charges. And not only the surface, but also all points of the conductor have the same potential.

Two characteristics of an electrostatic field.

Potential difference in two points is a quantitative characteristic of the field, equal to the strength. Both characteristics are unambiguously related. The field strength \(\overrightarrow{E}(x, y, z)\) is a function of the point. It determines the force acting on the charge. The field is fully set if the \(\overrightarrow{E}\) value in each of its points is known. Potential difference \(V(x_2, y_2, z_2) - V(x_1, y_1, z_1)\) - function of two points. It defines the work of moving the charge between these points. The field is fully set if the quantity of the difference of potentials between any two points is known.

What is the point of introducing another field characteristic along with the strength? ( Especially since it is less visible than strength.) The fact is that the potential or difference of potentials as a field characteristic has several advantages.

1. Field strength \(\overrightarrow{E}\) is a vector the value of which is determined completely by three independent values - vector projections on coordinate axes. Potential - scalar. Only one value is needed for its setting.

2. Just as the danger from a falling stone is directly determined not by the force of gravity at the Earth's surface but by the work performed by the field of gravity, many processes are determined not by the electric field strength in a given place, but by the difference of potentials. In particular, the potential difference is determined by such an important value as the force of electric current.

3. The difference of potentials is much easier to measure than the field strength. We will see this in the future in section 80.