77. Uniform electrostatic field potential

The work of a uniform electrostatic field.

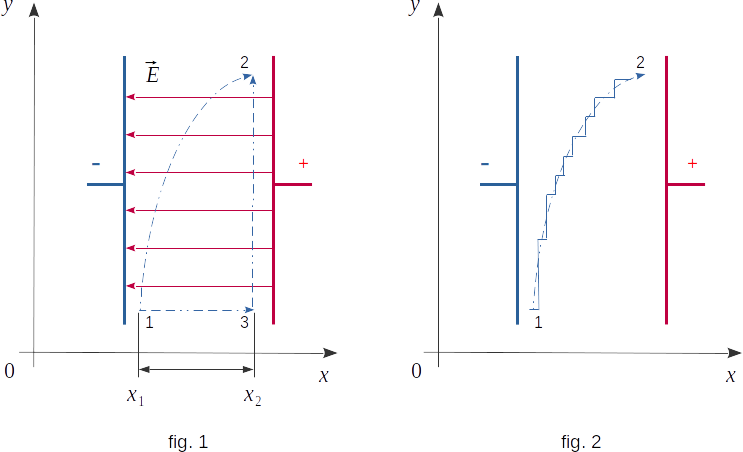
Consider the simplest case of an electric field - a uniform field. Such kind of field can be created by large plates charged with electric charges of the opposite sign, if the distance between the plates is much smaller than the size of the plates themselves (fig. 1).

Let's show with the help of calculations that the work done by the field when moving the positive charge from point 1 to point 2 really doesn't depend on the shape of the trajectory.

Let the movement first be performed on lines 1-3-2. On the line segment 1-3, the field will perform the work

\( \Delta{W} \,= \,-q\,E\,(x_2 - x_1) \) (8-19)

where \(x_2-x_1\) is the absolute value of the charge movement. The minus sign appears because the force acting on the charge is directed against the movement.

On the segment 3-2 the work is equal to zero, because the field is perpendicular to the movement. Therefore, the equation \((8-19)\) determines the full work when the charge \(q\) is moved from point 1 to point 2 on the line 1-3-2. Moreover, and most importantly, the work does not depend on the shape of the trajectory. If you move the charge \(q\) from point 1 to point 2 along an arbitrary curve 1-2, the work will also be determined by the equation \((8-19)\). Indeed, moving along the smooth curve can be replaced by moving along a stepped line with as few steps as possible in the calculation of the work (fig. 2). But at movement along the y axis work is not performed, as the power line field is perpendicular to movement. On the segments parallel to the x axis, the same work \((8-19)\) will obviously be performed. The work on the closed line 1-2-3-1 is equal to zero, as the negative work of the field on the segment 1-2 is equal to the positive work on the segment 2-3-1.

Potential charge energy in an electrostatic field.

When moving a body in the Earth's gravity field, the work is calculated in the same way. It does not depend on the shape of the trajectory and is equal to zero in a closed path. In mechanics, the work of gravity was represented by changing the potential energy. The same can be done in electrostatics. The equation \((8-19)\) can be represented in the form

\( \Delta{W} \,= \,-(q\,E\,x_2 - q\,E\,x_1) \)

If we now enter value

\( U \,= \,q\,E\,x \)

then

\( \Delta{W} \,= \,-{(U_2 - U_1)} \,= \,-\Delta{U} \)

The work therefore equals the change in \(U\) when the charge is moved from one point of space to another, taken with the reverse sign. This value is nothing more than potential energy of interaction of charge with uniform electrostatic field (or, what is the same, potential energy of interaction of charge \(q\) with charges on plates).

Potential (Voltage).

The potential energy of the charge/field interaction depends not only on the field itself, but also on the quantity of the charge. The ratio of potential energy to the quantity of the charge is independent of the charge and can therefore be considered as a characteristic of the electrostatic field. This relation is called electrostatic field potential at a given point

\( V \,= \,\frac{U}{q} \) (8-20)

For a uniform field

\( V \,= \,E\,x \) (8-21)

Potential difference.

Work on the movement of charge \(q\) from point 1 to point 2 can be written as follows

\( \Delta{W} \,= \,(U_2 - U_1) \,= \,-q\,(V_2 - V_1)\) (8-22)

From here, the potential difference equals

\( V_2 - V_1 \,= \,\Delta{V} \,= \,\frac{\Delta{W}}{q} \) (8-23)

Thus, the difference of potentials between two points is equal to the work on the movement of an electric charge from one point to another, taken with the reverse sign, referred to this charge.

The results obtained, expressed by equations \((8-20)\) and \((8-22)\) or \((8-23)\), are valid not only for the particular case of a uniform field but also for any electrostatic field in general. This follows directly from what is stated in section 76. But only the field potential in general will not be determined by equation \( V \,= \,Ex \). The dependence of the potential on the coordinates is determined by the location of the charges creating the field, and will change when this location changes.

It is important to understand that the physical sense has not the potential itself, but the difference of potentials (voltage). The potential of a given point can be put equal to any value. If an arbitrary constant \(C\) is added to the potential \((8-21)\), so that

\( V \,= \,E\,x + C\),

the potential difference between any points will not change. The potential, as well as the potential energy in mechanics, is determined with an accuracy to an arbitrary constant.

Point charge potential.

Let's give the equation for determination of field potential of point charge (in SI units)

\( V \,= \,\frac{q}{4\pi \,\varepsilon{_0} \,\varepsilon \,r} \,+ \,C \) (8-24)

Here \(C\) is an arbitrary constant. The constant \(C\) is usually taken equal to zero. This means that the potential at infinity (\(r \rightarrow \infty\)) is chosen to be zero.

Since the field of a uniformly charged sphere outside the sphere coincides with the field of a point charge located in the centre of the sphere, the equation \((8-24)\) for the point charge potential is fair and for the field of a uniformly charged sphere.