85. Connections of capacitors. Different types of capacitors

Very often capacitors are connected to each other in batteries. This makes it possible, with an existing set of capacitors, to obtain batteries of different capacities. The connection of the capacitors can be parallel and in series.

Parallel connection of the capacitors.

When two capacitors of \(C_1\) and \(C_2\) capacity are connected in parallel, their plates are connected in pairs with each other (fig. 1). The capacitance of the battery is understood as the ratio of the charge given to the battery to the potential difference between the capacitor plates. The potential difference \(\Delta{V}\) in parallel connection is the same for both capacitors. The charge of the battery is

\( Q \,= \,Q_1 \,+ \,Q_2 \)

where \(Q_1\) is the charge of the first capacitor and \(Q_2\) is the charge of the second capacitor. The battery capacity is equal to

\( C \,= \,\frac{Q}{\Delta{V}} \,= \,\frac{Q_1 \,+ \,Q_2}{\Delta{V}} \,= \,\frac{Q_1}{\Delta{V}} \,+ \,\frac{Q_2}{\Delta{V}} \)

Since

then

\( C \,= \,C_1 \,+ \,C_2 \)

When capacitors are connected in parallel, their total capacitance is equal to the sum of capacitance of individual capacitors. If \(n\) capacitors are connected in parallel, then

\( C \,= \,\sum\limits_{i}^{n} C_i \)

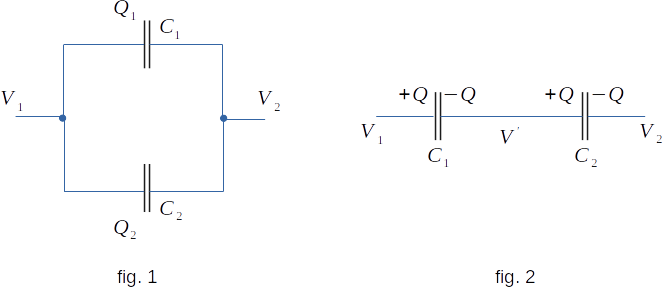
Serial connection of the capacitors.

Figure 2 shows the serial connection of two capacitors. In this case, the charges of both capacitors are the same. If the edge plate of the first capacitor has a charge of \(+Q\), then a \(-Q\) charge appears on the opposite plate due to the attraction. Since the wire between the capacitors and the plates connected by them are neutral as a whole, the charge of the inner plate of the second capacitor is equal to \(+Q\).
The battery capacity of the capacitors is

\( C \,= \,\frac{Q}{V_1 \,- \,V_2} \)

where \(V_1\) and \(V_2\) are potentials of the edge plates. The capacitance of the individual capacitors is equal to

where \(V^{'}\) is the potential of the plates connected by a conductor. Let's find the sum of the values, as inverse capacities of capacitors

\( \frac{1}{C_1} \,+ \,\frac{1}{C_2} \,= \,\frac{V_1 \,- \,V^{'}}{Q} \,+ \,\frac{V^{'} \,- \,V_2}{Q} \,= \,\frac{V_1 \,- \,V_2}{Q} \,= \,\frac{1}{C} \)

Therefore, at series connection the value, as inverse capacitance of the battery, is equal to the sum of values, inverse capacitance of individual capacitors. In general, for \(n\) capacitors, equality is

\( \frac{1}{C} \,= \,\sum\limits_{i}^{n} \frac{1}{C_i} \)

Different types of capacitors.

Depending on the purpose, the capacitors have different types of device and external design. A typical technical paper capacitor consists of two strips of stadium, isolated from each other by a paper tape soaked with paraffin. The strips and ribbon are tightly rolled up into a compact package of small size.

In radio engineering, capacitors with variable capacity are widely used. Such capacitor consists of two systems of metal plates, which can enter into one another when the handle is rotated. The area of the plates overlapping and, consequently, the capacitor capacity changes.

There are many other types of capacitors. Significant increase in capacitance by reducing the distance between the plates is achieved in so-called electrolytic capacitors. The dielectric in them is a very thin film of oxides that covers one of the plates (strips of foil). The second plate is another strip and the paper connected to it, soaked in a conductive substance solution (electrolyte). The oxide film is destroyed when the polarity of the voltage applied to the electrolytic capacitor changes. Therefore, before the capacitor is included in the circuit, it is necessary to check whether the potential difference sign in the given section of the circuit corresponds to that required for the given capacitor.