45. Dependence of pressure and density of saturated vapour on temperature

The diagram of equilibrium states of gas and liquid (Fig. 4) shows that the higher the temperature, the higher the pressure of saturated vapour. Therefore, the pressure of saturated vapour does not depend on the volume, but only on the temperature. This dependence of \(p(T)\), found experimentally, is shown in Figure 1. It is not linear, as is the case with ideal gas at a constant volume. The slope of the curve expressing the dependence of \(p(T)\) on the T-axis is greater when the temperature is higher. Consequently, the pressure at higher temperatures increases with temperature rise faster than at lower temperatures. On the other hand, the state of vapour up to saturation can be approximately described by the ideal gas equation (1-12)

\( pV = \frac{m}{\mu}RT \)

As the temperature rises the increase in saturated vapour pressure is faster than in ideal gas for the following reason.

When the liquid with vapour in a closed container heats up, part of the liquid is vaporized. As a result, the density of vapour rises, so that a slight increase in the volume occupied by vapour is followed by a significant increase in its mass. As a result, the pressure increases not only by increasing the temperature, but also by increasing the density of vapour. When all the liquid has evaporated, the vapour will no longer be saturated with further heated and its pressure will be linearly dependent on temperature (Fig. 2).

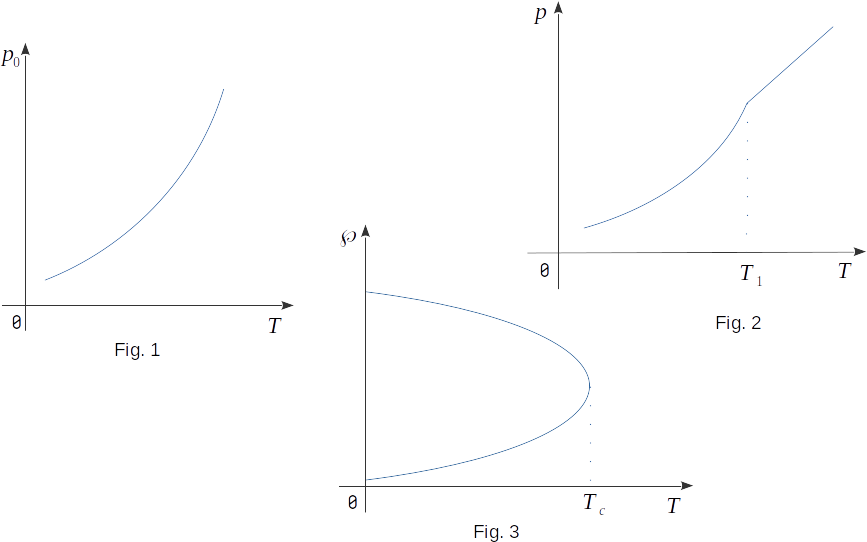
At the same time as the pressure of saturated vapour increases as the temperature increases, so does the density of the vapour. On the contrary, the density of the liquid in equilibrium with its vapour decreases with the expansion of the liquid during heating. If we draw in one figure the curves of the liquid density and its vapor dependence on temperature, the curve will go down for the liquid and up for the vapor (Fig. 3). At critical temperature both curves merge, i.e. the density of the liquid becomes equal to the density of vapour. The difference between liquid and vapour disappears.