37. Potential energy of interaction between two molecules

Introduction to the interaction of molecules began with a review of forces. However, it is more important to know not the forces, but the potential energy of molecular interaction. In the case of a large number of molecules (and in a macroscopic body this number is huge) the main role is played the energy. It is possible to speak, about average energy of molecules of substance (it is internal energy), but to speak about average force of interaction does not make sense. Forces between separate pairs of particles are equal in quantity, and are directed to each other. Therefore, the total sum of forces acting inside any body is equal to zero at all. We can only speak about the average force with which the system (for instance, gas in a cylinder) acts on the outer body (for example, on the walls of a cylinder).

By knowing the dependence of force on distance, it is possible to determine the exact dependence on distance the potential energy. But it is enough for us to know only approximately the type of potential curve \(U(r)\). First of all, let's remember that the potential energy is determined with an accuracy to an arbitrary constant, because it is not the potential energy itself that makes sense, but the difference of potential energies in two points, equal to the work taken with the opposite sign. Let's consider, as it is accepted in physics, that \(~U = 0\) at \(r \rightarrow \infty\). The potential energy of the system can be considered as the value of the work that the system can do. And the potential energy is determined by the location of bodies, but not by their velocities. The greater the distance between the molecules, the more work will be done by the attraction forces between them at their approach. Therefore, with decreasing \(r\), starting from the initial large values, the potential energy will decrease. At \(r ~\rightarrow ~\infty\) the potential energy is equal to zero. That is why at decreasing \(r\) the potential energy becomes negative (Fig. 2).

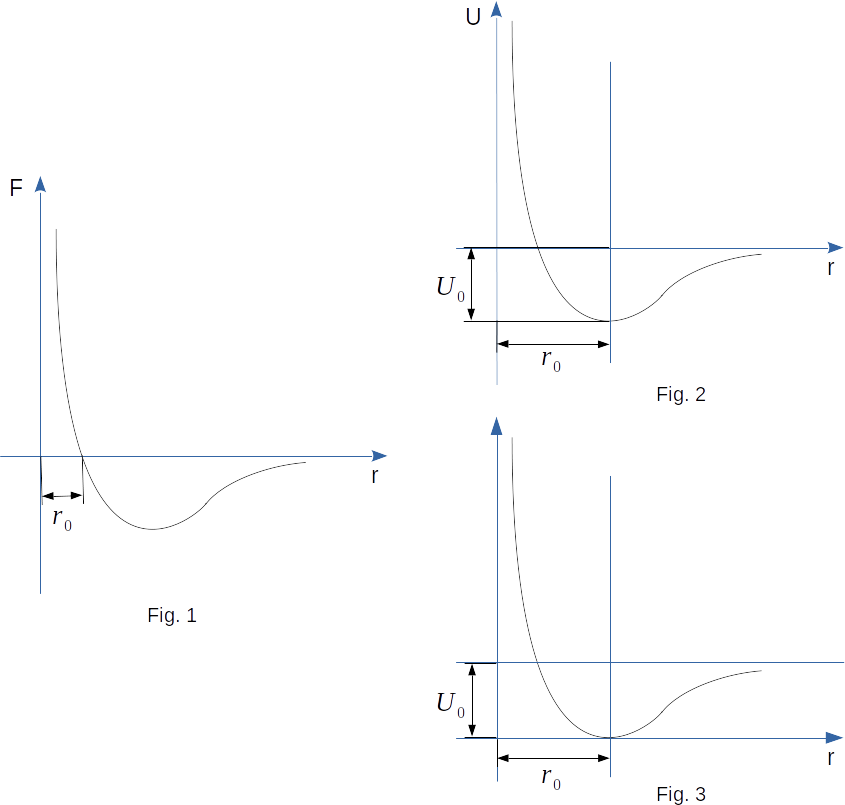
In the point \(r = r_0\) the force is equal to zero (Fig. 1). Therefore, if the molecules are located at this distance, they will rest. And the system cannot perform any work. It means that at \(r = r_0\) the potential energy has a minimum. We could take this value of potential energy \(-U_0\) as the initial value of potential energy. Then it would be positive everywhere (Fig. 3). Both curves (Figs. 2 and 3) equally characterize the interaction of molecules. The difference of \(U\) values in two points is the same for both curves, and only this difference makes sense.

At \(r < r_0\), rapidly growing repulsive forces appear. They can also perform work. Therefore, the potential energy is growing as the molecules come closer together. And it grows very fast.

Knowledge about the dependence of the potential energy interactions of molecules from the distance between them allows us to establish quantitative differences between gases, liquids and solids in terms of molecular-kinetic theory. In gases, the average kinetic energy of molecules is greater than the absolute value of the average potential energy. That is why the attraction forces cannot hold the gas molecules against each other. In liquids, the average kinetic energy of molecules is less than the absolute value of the average potential energy, and in solids it is much less.