36. The interaction forces of molecules

Ideal gas molecules are not attracted to each other. That is why the ideal gas does not turn into a liquid at any temperature. The formation of liquid or solid bodies is obviously only possible through the attraction of molecules. Otherwise, the molecules would spread out in all directions. In order to understand why real gas turns into liquid or solid body during cooling, it is necessary to get to know the interaction of molecules (or atoms) in more detail.

A molecule is a complex system consisting of individual charged particles: electrons and atomic nuclei. Although in general molecules are electrically neutral, significant electrical forces act between them at short distances. There is an interaction between electrons and nuclei of neighboring molecules. Description of the motion of particles inside atoms and molecules and the forces of interaction between molecules is a very complex task. It is considered in atomic physics and solved with the help of quantum mechanics. We will only give the final result: an approximate dependence of the interaction force of two molecules on the distance between them.

This force is quite complex to change as the distance changes. At distances several times greater than the size of the molecules, there is a force of attraction between them. These forces increase as the molecules approach. But at very short distances the attraction forces begin to decrease, and when the molecules come close to each other, repulsive forces arise between them. Without repulsive forces at very short distances, the substance could not exist. The molecules would penetrate into each other and the entire piece of matter would shrink to the volume of one molecule.

Figure 1 shows an approximate relationship between the interaction force of the two molecules and the distance between them. Negative force values correspond to the attraction and positive force values to repulsion. At a distance \(r_0\) equal to approximately the sum of the molecule radii, the interaction force is zero. With \(r \rightarrow \infty ~F \rightarrow 0\), and with \(r \rightarrow 0 ~F \rightarrow \infty\).

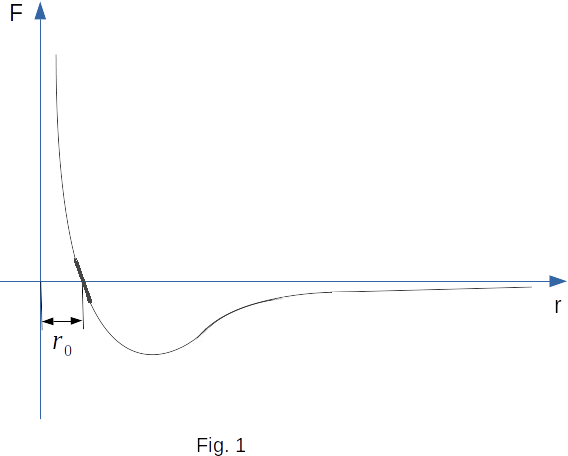
The dependence of the interaction forces of molecules on the distance between them explains the appearance of elasticity forces in the compression and tension of bodies. If we try to bring the molecules closer to each other by a distance smaller than \(r_0\), there will be a force preventing them from coming closer. On the contrary, when the molecules are separated from each other, there is a force of attraction, which returns the molecules to their original positions after the end of the external influence.

When molecules are displaced slightly from the equilibrium position the attraction or repulsion force grows linearly with increasing displacement. In a small segment, the curve can be considered as a straight segment (the thickened section of the curve in Fig. 1). That is why Hooke's law, according to which the elastic force is proportional to the amount of deformation, is true for small deformations. At large displacements of molecules Hooke's law is already unfair.

Since the deformation of the body changes the distances between all molecules, the neighboring layers of molecules have a small part of the total deformation. Therefore, Hooke's law is applied at deformations millions of times larger than the size of the molecules.