10. Ideal gas equation of state

All gases are subject to the basic gas laws only approximately, and less precisely if higher the density of gas and lower the temperature. Gas, which would be exactly subject to the gas laws established in sections 5-8, is called ideal. All real gases are more or less different in their properties from the ideal gas. Experiments show that hydrogen is the closest to ideal gas.

Using gas laws, we can get an ideal gas equation of state, i.e. an equation which connects all three values \(p\), \(V\) and \(T\) that characterize the state of a given mass \(m\) of a certain gas.

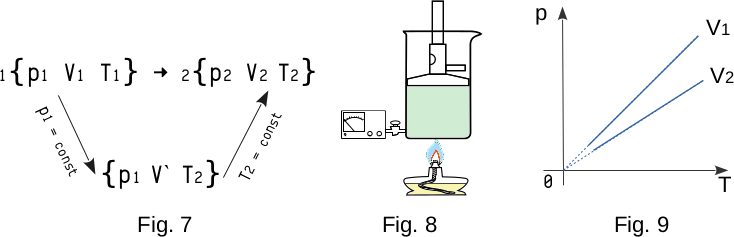
Suppose that in the initial state 1 some mass of gas \(m\) has the pressure \(p_1\), volume \(V_1\), and temperature \(T_1\) (Fig. 7). Then the gas goes to a new state 2, at which pressure, volume and temperature have new values \(p_2\), \(V_2\), \(T_2\). What is the relationship between these three values in the initial and final states?

Let's pass gas state 1 to state 2 in two steps. First, at a constant pressure of \(p_1\), we will change the gas temperature to \(T_2\). The volume of it will be equal to some new value of \(V{'}\). Then, isothermally, i.e. at \(T_2 = const\), we transfer the gas to the final state with the pressure \(p_2\), and the volume \(V_2\).

According to Charles's law (1-7) the relation of volume \(V\) to temperature \(T\) at the given pressure is the same, then

\( {V{'} \over T_2} = {V_1 \over T_1} \)

or

\( V{'} = {V_1 {T_2 \over T_1}} \) (1-8)

Next, we use the Boyle-Mariotte law (1-1)

\( p_1 V{'} = p_2 V_2 \) (1-9)

By replacing \( V{'} \) in equation (1-9) from equation (1-8), we get

\( {p_1 V_1 \over T_1} = {p_2 V_2 \over T_2} \)

and this result does not depend on the way of transition from the initial state 1 to the final state 2. We come to the conclusion
For a given mass of gas, the ratio of pressure and volume to absolute temperature is a constant value which is independent from state of gas, where gas is located

\( {p V \over T} = k = const \) (1-10)

Equation (1-10) is called the Clapeyron equation and it is one of the forms of the ideal gas equation of state. Constant \( k \) depends on the mass and type of the gas.

From equation (1-10), when the gas is heated in a hermetically closed container (Fig. 8) gas pressure will increase proportionally to the absolute temperature if the volume does not change

\( p = {k \over V} T \)

This dependence of gas pressure from temperature at a constant volume is called Gay-Lussac's law. In order to test this law by experiment, it is necessary to heat the gas in the container with observing changes in pressure and temperature. The process is called isocharian and the lines that represent the pressure dependence on temperature of a given gas mass are called isochoric. (Fig. 9, where \( V_1 < V2 \))

Using the Avogadro law, we can find the dependence of constant k from the gas mass and its molar mass. If the mass of the gas is equal to one mole, then at \(p_0 = 1 \, atm \) and \( T_0 = 273^0 \, K\) the volume of any gas \(V_{0\mu} = 22.4 \, l/mol \) (index \( \mu \) indicates that the mass of the gas is equal to one mole). Hence, mole for any gas

\( {p V_\mu \over T} = {p_0 V_{0\mu} \over T_0} = {{1 \, atm \, \times \, 22.4 \, l} \over {273 \, K \, \times \, mol}} = R \) (1-11)

The \(R\) constant is the same for all gases and is called a universal gas constant. Its value depends only on the selection of the unit system

\( R = 0.082 {{atm \, l} \over {K \, mol}} = 8.31 \times 10^7 {erg \over {K \, mol}} \)

The International System of Units (SI)

\( R = 8.31 \times 10^3 {J \over {K \, kmol}} \)

If the mass of the gas is not one mole, but a certain number \( n = {m \over \mu} \), then at the same pressure and temperature as for one mole, the volume

\( V = V_\mu n = {m \over \mu} V_\mu \)

Multiplying equation (1-11) by \( m \over \mu \), we get the molar form of the ideal gas equation of state.

\( p V = {m \over \mu} R T \) (1-12)

It was first stated by Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law.
The dependence of the equation of state from gas type appears only through its molecular mass.
All main gas laws are presented in equation of state (1-12). When considering a mixture of gases, it is also necessary to use Dalton's law. This law, together with equation (1-12), makes it possible to find an equation of state for any mixture of gases.