12. Work in Thermodynamics

Now we will learn more about the process of changing the state of the body or body system. There are two significantly different types of effects that lead to changes in the state of bodies. First of these is to perform the work.

Assume that the system under consideration is the gas in the cylinder under the piston (fig. 10). You can change the volume, pressure and temperature of the gas by moving the piston down. In this case, the change in gas state is a result of macroscopic movement of the body (piston) acting on the system. In this case, the force with which the piston acts on the gas, performs the work. Let's calculate this work.
From the gas side, the force acts on the piston

\( F = pA \) (1-13)

where \(p\) is the gas pressure, \(A\) is the piston area. The same magnitude, but opposite force affects on the gas from the piston side.

If the piston moves to a small section h, the pressure can be considered constant, and then the elementary work performed on the gas is equal to

\( \Delta W = pA \Delta h \)

But \( A \Delta h = V_1 - V_2 \), where \(V_1\) is the initial volume and \(V_2\) is the final volume of the system. If the volume change writes as \(\Delta V = V_2 - V_1 \), then \( A \Delta h = \Delta V \). From this, the work connected with the system volume change follows

\( \Delta W = -p \Delta V \) (1-14)

It follows that when the gas is compressed \( \Delta V < 0 \), the external force does a positive work. When expanding \( \Delta V > 0 \), this work is negative.

Equation (1-14) defines the work done on gas. The work performed by gas \( \Delta W'\) has the opposite sign, \( \Delta W' = - \Delta W \).

Equation (1-14) is valid not only for compression or expansion of gas in the cylinder, but also for changes in the volume of any system on value \( \Delta V \).

To calculate the work when changing the volume to a finite (not as small as we like) value we need to sum up the elementary work (1-14). Only if \( p = const \) equation (1-14) is valid for large volume changes.

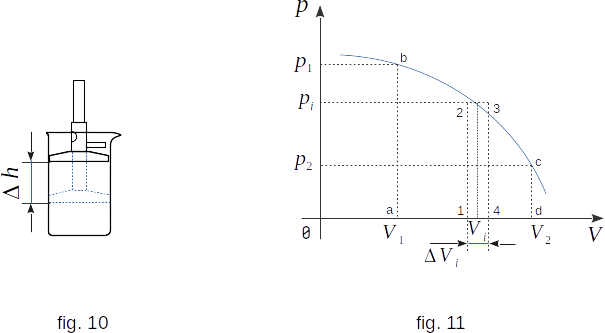
The work that the body does when it changes volume can be understood visually. If you draw a graph of the volume dependence from pressure (fig. 11), the area limited by this graph, with the axis \( V \) and the sections \( ab \) and \( cd \) which equal to the pressures \( p1 \) in the initial and \( p2 \) in the final states, will be numerically equal to the work with the volume change from \( V_1 \) to \( V_2 \). In fact, the work at small changes in the volume \( \Delta V \) is numerically equal to the area of the rectangle \( 1-2-3-4 \), because \( W'_i = p_i \Delta V_i \) (where \(p_i \) is pressure at volume \( V_i \)). The full area of the figure \( a-b-c-d \) can be considered as the sum of the areas of these elementary rectangles.