From the Direct electric current
97. Ohm's law for a closed circuit
Let's consider the simplest closed circuit consisting of galvanic element with EMF \(\,\mathcal{E}\,\), resistance \(\,r\) (this resistance of the element is called its internal resistance) and external resistance \(R\) (fig. 1). Ohm's law for a closed circuit links the electric current force in the circuit, the EMF and the total resistance of the circuit. This connection can be established theoretically by using the energy conservation law and the Joule-Lenz law.
Let the charge \(Q\) pass through the cross section of the conductor in time \(t.\) Then the external forces will do the work
\( W_1 \,= \,Q\,\mathcal{E} \,= \,I\,t\,\mathcal{E} \) (9-7)
Because of this work \(\,W_1,\,\) on the internal resistance of the element \(r\) and the external resistance of the circuit \(R\), released the quantity of heat equal to the law of Joule-Lenz
\( W_2 \,= \,I^2\,R\,t + I^2\,r\,t\)
By equating this expression to the work of external forces \((9-7)\) on the basis of the law of energy conservation, we obtain
\( \mathcal{E}\,I\,t \,= \,I^2\,R\,t + I^2\,r\,t\)
From here follows Ohm's law for closed circuit
\( I \,= \,\frac{\mathcal{E}}{R \,+ \,r} \) (9-8)
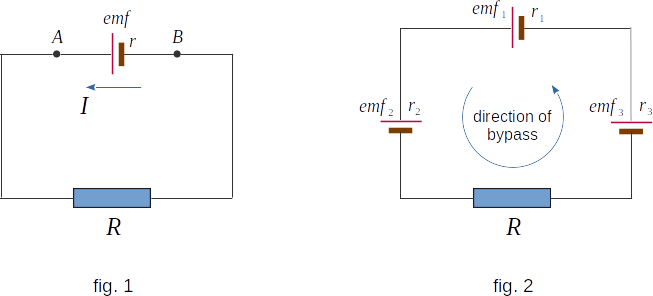
If the circuit contains several elements in series connected with EMF \(\,\mathcal{E}_1, \mathcal{E}_2, \mathcal{E}_3\,\), and so on (fig. 2), then the complete EMF of the circuit is equal to the algebraic sum of EMF of the individual elements
\( \mathcal{E} \,= \sum\limits_{i=1}^{N} \mathcal{E}_i \)
The value of \(\mathcal{E}_i\,\) is included in this sum with a "plus" sign. If we bypass the circuit in an arbitrarily chosen direction (for example, counterclockwise) we pass from the negative pole of the element to the positive pole (external forces inside the battery are directed from minus to plus), and with a "minus" sign - otherwise. So, for the circuit shown in Figure 2