88. Electric current force and density

It is convenient to characterize the electric current on the quantitative side with two values. One of them is familiar to you from the physics of book one. In the presence of electric current through any cross section of the conductor is continuously transferred electric charge (fig. 1). Let the amount of electricity \(\Delta{Q}\,\) pass through the cross-section of the conductor in time \(\Delta{t}\). The ratio of this amount of electricity to the time interval \(\Delta{t}\,\) is the average amount of electricity that passes through the cross-section of the conductor in the one unit of time. This value is called electric current force

\( I \,= \,\frac{\Delta{Q}}{\Delta{t}} \) (9-1)

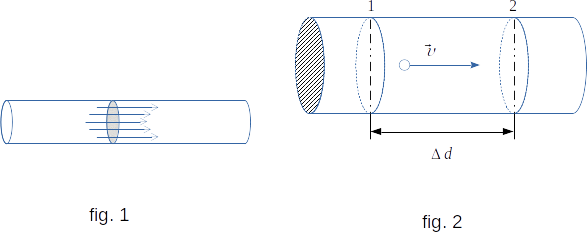
The value of the charge passing through the cross-section of the conductor is related to the number of moving particles and to their charge. Let the conductor has a cylindrical form (fig. 2). In the volume limited by two cross-sections \(1\) and \(2\), is concluded \(n\,\Delta{d}\,A\,\) particles, where \(n\) - the number of charged particles in an one unit of volume. Counting that the particles move from left to right at an average velocity \(\overrightarrow{\upsilon}\), we obtain that during the time \(\Delta{t} \,= \,\frac{\Delta{d}}{\upsilon}\,\) all particles contained in this volume will pass through section \(2\). Consequently, during this time will be transferred through the conductor section the charge

\( \Delta{Q} \,= \,q\,n\,\Delta{d}\,A \)

where \(q\,\) is the charge of one particle. Then the current force

\( I \,= \,\frac{\Delta{Q}}{\Delta{t}} \,= \,q\,n\,\upsilon\,A \) (9-2)

The electric current force can be either positive or negative. If a certain direction in the conductor (for example, from left to right) is chosen as positive, \(I > 0\,\) when the electric current flows in this direction, and \(I < 0\,\) when the electric current flows in the opposite direction. Thus, the current sign depends on the choice of the positive direction in the conductor or in the conductive circuit.

Along with the electric current force, another characteristic, electric current density, is used. The average electric current density is equal in value to the ratio of electric current force to the cross-sectional area of the conductor, provided that the cross-sectional area is perpendicular to the average speed of the directed motion of particles

\( j \,= \,\frac{I}{A} \)

In contrast to the electric current force, current density is by definition a vector directed along the average particle velocity. Taking into consideration \((9-2)\), we obtain

\( \overrightarrow{j} \,= \,q\,n\,\overrightarrow{\upsilon} \) (9-3)

In the international system of units current force is measured in amperes. This unit, along with the meter, second, kilogram and degree (temperature) is the main unit. How it is set we will tell later, when it comes to magnetic interactions.

The current density in this system of units is measured in amperes per meter in square \((a/m^2)\).