128. Effects of a magnetic field on a moving charge. The Lorentz force

Electric current is always the movement of electric charges. Therefore, it is natural to consider that the action of a magnetic field on a conductor with an electric current is the result of the field action on a set of moving charges. The impulse given by the magnetic field to moving charges is transmitted by collisions to ions of a crystal grid metal or to electrolyte molecules.

The electric field acts on a charge with force \(\overrightarrow{F_e}=q\overrightarrow{E}\). Consequently, if there is both an electric field and a magnetic field, the whole force acting on the charge will be equal to

\( \overrightarrow{F} \,= \,\overrightarrow{F}_e \,+ \,\overrightarrow{F}_m \)

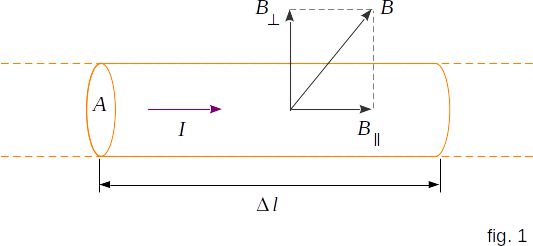
Let's find the \(\overrightarrow{F}_m\). For this purpose we will consider a piece of a thin direct conductor with an electric current (fig. 1). Let length \(\Delta{l}\) and cross section \(A\) of the conductor segment will be so small, that the vector induction of the magnetic field \(\overrightarrow{B}\) can be considered invariable in limits of this segment of the conductor. The current \(I\) in the conductor is connected with the value of the particle charge \(q\), the concentration of charged particles (the number of charges in a unit of volume) \(n\) and the speed \(\upsilon\) of their ordered motion by equation (go to \(\S 88\))

\( I \,= \,q\,n\,\upsilon\,A \) (11-4)

The force acting from the magnetic field side on the selected conductor segment with electric current is equal to

\( F_m \,= \,I\,\Delta{l}\,B\,sin{\alpha} \)

Substituting here the equation \((11-4)\) for the current, we obtain

\( F_m \,= \,q\,n\,\upsilon\,A\,\Delta{l}\,B\,sin{\alpha} \,= \,\upsilon\,q\,N\,B\,sin{\alpha}\)

Where \(N=nA\Delta{l}\) is the number of charged particles in the considered volume.
Consequently, for each charge from the side of the magnetic field acts force

\( F_m \,= \,q\,\upsilon\,B\,sin{\alpha} \)

This force is perpendicular to vectors \(\overrightarrow{B}\) and \(\overrightarrow{\upsilon}\), and its direction is determined using the same rule of the left hand.
If the left hand is placed so that the component of the magnetic induction vector \(B_{\perp}\), perpendicular to the velocity of the charge, entered in the palm (or, in other words, the induction lines would enter in the palm), four fingers were directed in the movement of positive charge, then a 90 degree bent thumb will show the direction of the force \(\overrightarrow{F}_m\), acting on the charge (fig. 2). \(\overrightarrow{F}_m\) is called the Lorentz force.