125. Magnetic field of current

Using a small frame with an electric current makes it possible to experimentally determine the induction vector \(~ \overrightarrow{B}\,\) at each point of the field. For example, it is possible to find the magnitude and direction of the magnetic field of any conductor with electric current.

Here, first of all, it is found that the magnetic field is essentially dependent on the medium that fills the entire space around the conductor with electric current. The value of the magnetic induction vector \(~ \overrightarrow{B}\,\) in the presence of a uniform medium differs by a certain number of times from the value of the vector \(~ \overrightarrow{B_0}\,\) at the same point in a vacuum (free space). The ratio \(~ \frac{B}{B_0} \,= \,\mu \,\) characterizing the magnetic properties of the medium is called magnetic permeability of medium.

Now leaving the medium unchanged and setting the electric current in the conductor at one constant value, we will change the shape of the conductor. Here we can make sure that the change in the shape of a closed conductor with current has a significant impact on the magnitude and direction of vector \(~ \overrightarrow{B}\,\) at a given point.

It is not difficult to understand the reason of such influence. The matter is that the magnetic field in each point is created by all sections of the closed conductor with a current. The magnetic induction vector \(~ \overrightarrow{B}\,\) at a given point can be represented as a geometric sum of magnetic induction vectors \(\Delta\overrightarrow{B_i}\), created by individual sections of the conductor. Changing the location of individual sections leads to changes in a number of vectors of such sum and therefore affects the magnitude and direction of vector \(~ \overrightarrow{B}\,\) at a given point.

If it is known which part of magnetic induction \(~ \overrightarrow{B}\,\) creates each individual segment, it is possible to calculate the magnetic field of any conductor with current.

The formula from which it is possible to determine the magnetic induction vector \(\Delta\overrightarrow{B_i}\), created by individual element with current, was established experimentally by the French scientists Biot and Savart, and is called the Biot-Savart Law.

The direction of the vector \(\Delta\overrightarrow{B_i} \,\) is determined by the right screw rule. The arm of the drill turns in the direction where the magnetic field of the element is directed if the drill itself moves along the current (fig. 1).

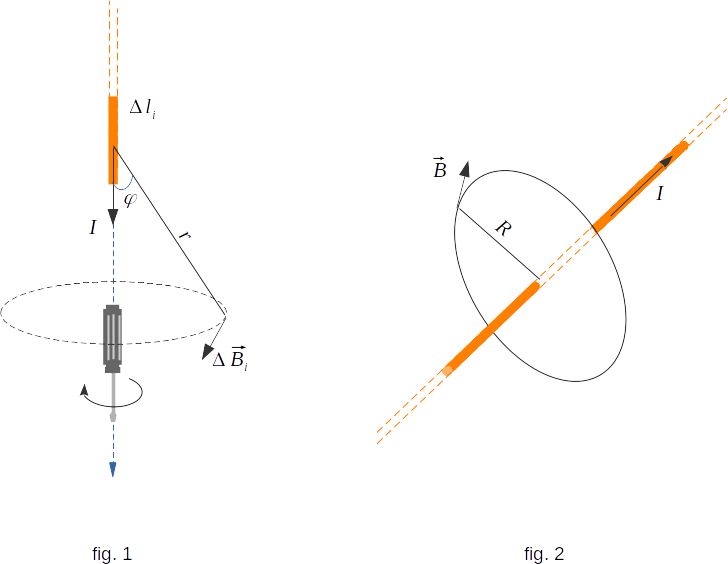
Calculations by the formula of Biot-Savart and experimental studies give the following equation for the magnitude of induction of the magnetic field of infinite direct-linear conductor with a current in a uniform medium with magnetic permeability \(~ \mu \) (fig. 2):

\(B \,= \,\mu\mu_0\frac{I}{2 \pi R} \)

Here \(~R\,\) is the distance from the conductor to the point in which the magnetic induction is calculated. The conductor can be considered infinite if its length is many times greater than the distance \(~ R\). The direction of vector \(~ \overrightarrow{B}\,\) is determined, as usual, by the right screw rule. Magnetic constant \(\mu_0\), is called magnetic permeability of free space. The magnetic permeability of free space is taken to have the exact value \(\mu_0 \,= \,4\pi \times 10^{-7} \,N/A^2 ~or ~T \cdot m/A\).