From the Magnetic field of currents
127. Interaction of parallel currents. Unit of force current - Ampere
Knowing the induction of the magnetic field \(~ \overrightarrow{B}\,\), created at any point of space by a closed conductor with an electric current, you can use equation \((11-2)\) to calculate the force acting on a segment of another wire with an electric current placed at the same point. By summing up the forces acting on the individual sections, we obtain the force acting on the entire wire. This force will be the force of the magnetic interaction of currents.
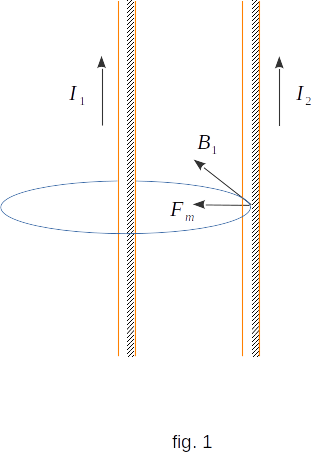
Let's consider the interaction of two parallel infinitely long conductors with the current, located at a distance \(~ R\,\) from each other. We know already (\(\S\) 125), that the long straight conductor, on which the electric current \(~ I_1 \,\) flows, creates at distance R from the wire magnetic field
\(B_1 \,= \,\mu\mu_0\frac{I_1}{2 \pi R} \)
Any segment of the length \(~ l\,\) of the other conductor, if current \(~ I_2 \,\) flows through it, tests in this field the force determined by equation \((11-2)\). Applying the rule of drill (right screw), it is easy to verify that the vector \(~ \overrightarrow{B}\,\) in all points perpendicular to the second wire with a current (fig. 1). Consequently, the force acting on the segment with the length \(~ l\,\) of other wire is perpendicular to it and equal to
\( F_m \,= \,I_2\,B_1\,l \,= \,\mu\mu_0\frac{I_1 I_2}{2 \pi R}l \) (11-3)
This force lies in the plane of both wires and is a force of attraction if the electric currents of the conductors are directed in the same direction, or a force of repulsion if the currents are opposite.
The main action of an electric current is its magnetic action. Therefore, it is the magnetic action was used to establish the unit of current force. In the SI system, the unit of current force - Ampere is the fourth main unit (along with meter, kilogram and second). It is determined by the magnetic interaction of parallel currents.
Ampere is a direct current force, which, passing through two parallel conductors of infinite length and very small circular cross-section, located at a distance of 1 meter one from another in a vacuum, would cause between these conductors a force equal to \(2 \cdot 10^{-7} \,N\) per each meter of the length of the conductor.
Substituting in equation \((11-3)\) \(F=2 \cdot 10 \,N\), \(~ \mu=1\) (vacuum), \(~ I_1=I_2=1 \,A\), \(~ R=l=1 \,m\), we obtain the value of magnetic constant \(\mu{_0}\)