34. Internal energy of a single atomic gas. Adiabatic process in gas

The easiest ideal gas in terms of its properties, consisting not of molecules, but of single atoms. Such a gas is called a monatomic or single atomic. This term implies that the "molecule" of gas consists of one atom. Helium, neon, argon are monatomic inert gases.

Ideal gas molecules do not interact with each other, except in cases of direct collision. Therefore, their average potential energy of interaction is very small and all internal energy represents the kinetic energy of chaotic movement of molecules.
Since the average kinetic energy of a molecule at translational motion is determined by equation \((3-12)\), the average kinetic energy for one mole is equal to

\(U ~= ~N_A\frac{3}{2}kT ~= ~\frac{3}{2}RT \)(3-14)

This equation defines the internal energy of an ideal single atomic gas.

When writing down the equation \((3-14)\), it was assumed that the container of gas rested, i.e. the velocity of the center of gravity of the gas is equal to zero. Therefore, the internal energy is the average kinetic energy of molecules movement relative to the center of gravity. This was already mentioned in \(\S16\). If the center of gravity of the gas moves at the speed of \(~\upsilon_0\), the total energy of one mole of gas is equal to the sum of mechanical (kinetic) energy \(~\frac{\mu\upsilon{^2_0}}{2}\) and internal energy \(U\)

\(\overline{E} ~= ~\frac{\mu\upsilon{^2_0}}{2} + \frac{3}{2}RT \)

The internal energy of an ideal gas consisting of more complex molecules is also proportional to the absolute temperature. But the proportionality coefficient between \(U\) and \(T\) is different.

Now let's discuss the difference between isothermal and adiabatic processes.

We will use two cylinders filled with gas. In the initial position \(1\) the volumes and temperatures of gas in the cylinders are the same. Then the gas expands. In the first cylinder, expansion occurs at a constant temperature - isothermally. The second cylinder is thermally insulated, so it has an adiabatic process.
In the isothermal process, the temperature and therefore the internal energy do not change. The pressure at expansion decreases by the Law of Boyle-Mariotte (Fig. 1).

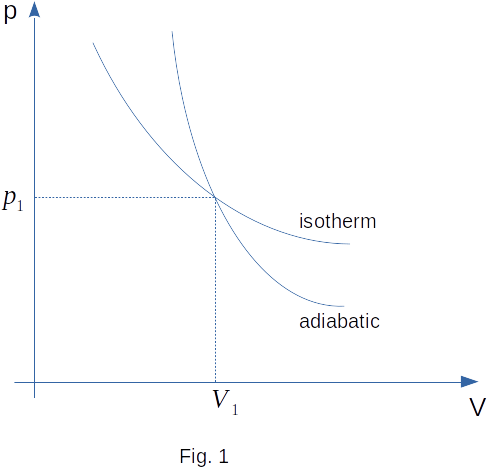
At expansion of gas in the thermally insulated \((\Delta{Q}=0)\) cylinder work is performed by internal energy of gas, so the internal energy is reduced. On the basis of equation \((3-14)\) we conclude that the temperature decreases as well.

Thus, with adiabatic expansion, the gas is cooled down. The pressure drops faster than with isothermal expansion (Fig. 1).
With adiabatic compression, work is done to increase the internal energy. Therefore, the temperature rises and the pressure rises faster than with isothermal compression (Fig. 1).