29. Basic equation of molecular-kinetic theory of gases

Lets find the dependence of the average gas pressure on the walls of the vessel on the average speed of its molecules.
Let the gas be in a rectangular vessel with solid walls of volume \(V\) (Fig. 1). Moreover, the gas and the vessel have the same temperature, i.e. are in thermal equilibrium.

Gas molecules collide with the walls of a vessel. Each time a molecule hits the wall, the molecule briefly interacts with the wall. We will consider the collisions of molecules with the walls to be absolutely elastic and calculate the impulse of force acting on the \(CD\) wall by the impact of one molecule. For this purpose we use the second Newton law.

The wall is the ideal reflector for an absolutely elastic impact. On the side of the wall, a force perpendicular to the wall acts on the molecule. A particle flying at a certain speed against the wall will fly away at the same speed after the collision. And if the projection of speed in the direction \(x\) is \(+\upsilon_x\) when moving towards the wall, then after reflection from the wall it will be \(-\upsilon_x\). Projections \(\upsilon_y\) and \(\upsilon_x\), on the other hand, do not change in value by elastic impact (Fig. 2). (Here \(\upsilon_x, \, \upsilon_y, \, \upsilon_z\) are the absolute values of the velocity projections.)

Let's denote the mass of the molecule \(m\), and the impact time (it is very short) \(\delta{t}\). Then, according to the second Newton law, the impulse of force \(f'\delta{t}\) acting on the molecule is equal to the difference between the projections of the molecule momentum on the \(x-axis\) after the collision (\(-m\upsilon_x\)) and before the collision (\(+m\upsilon_x\))

\(f'\delta{t} {~=~} (-m\upsilon_x) {~-~} (+m\upsilon_x) {~=~} -2m\upsilon_x \)

According to the third Newton's law, from the side of the molecule on the wall will act force \(f\), the impulse of which is equal to

\(f\delta{t} {~=~} 2m\upsilon_x \)

But we are not interested in the force acting on the wall by the impact of one molecule, but the average on time the force value, which is caused by the impact on the wall of all molecules in the time interval \( \Delta{t} {~\gg~} \delta{t} \). During this time, the wall will reach only those molecules that are at a distance not exceeding \( \upsilon_x\Delta{t} \) (Fig. 3). Otherwise, the molecules simply do not reach the wall in time. It should also be assumed that the \(CD\) walls will reach only those molecules with \( \upsilon_x \, > \, 0 \), i.e. moving from left to right.
(Thank you friendsThe interval \(\Delta{t}\) can be considered quite small, so that there are practically no collisions of molecules in the \( \upsilon_x\Delta{t} \) layer, even though the number of molecules is high. This is possible because the average distance between the molecules is much less than the average free path of the molecules, i.e. the average distance between the molecules without collisions.)

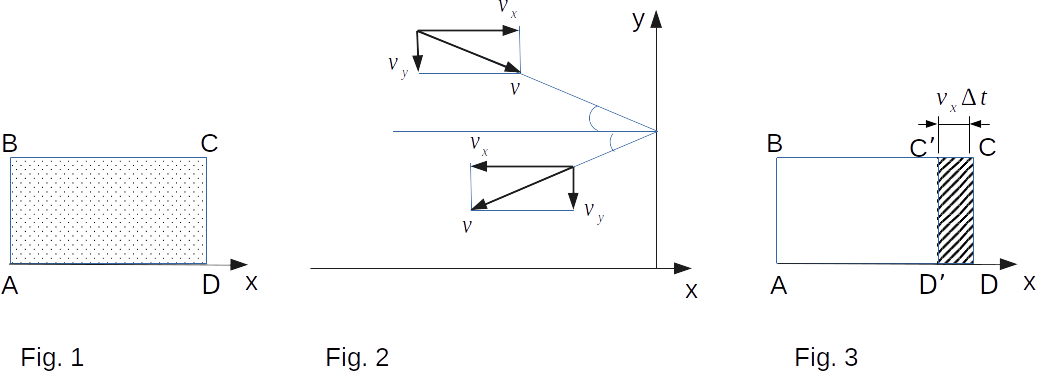
Do not think that the values of the velocity projections \( \upsilon_y \), and \( \upsilon_z \), somehow affect in achieving the molecules on the \(CD\) wall. If the molecule collides with the wall \(BC\) or \(AD\) (Fig. 3), the projection of the velocity \( \upsilon_x \) will not change and the molecule will still move along the axis \(x\) to the segment \( \upsilon_x\Delta{t} \).

The number of molecules \(n'\) in the allocated volume of \(CC'DD'\) is equal to

\(n' {~=~} nS \upsilon_x \Delta t \)

where
\(S\) is the CD wall area;
\(n {~=~} \frac{N}{V} \) average number of molecules per volume unit (concentration of molecules).

But only half the molecules are moving towards the wall of the \(CD\). Therefore, the number of hits of \(Z\) molecules against the wall of the vessel during the time \(\Delta t \) will be equal to

\(Z {~=~} \frac{n}{2} S \upsilon_x \Delta t \)

Each molecule gives a \(2m \upsilon_x \) impulse to the wall, and therefore during the time \(\Delta t\) the wall will receive impulse

\( F \Delta{t} {~=~} Z\cdot2m\upsilon_x {~=~} nmS \upsilon{^2_x} \Delta{t} \)

Now we have to consider that not all molecules have the same speed \(\upsilon_x\). The impulse of average force \({\overline F}\Delta{t}\) is defined by the average square of the velocity projection \(\upsilon{^2_x}\)

\( {\overline{F}}\Delta{t} {~=~} nmS \overline\upsilon{^2_x} \Delta{t} \)(3-7)

Now let's use the equation \((3-6)\) to enter the average square of velocity \(\overline\upsilon^2 \). Then, dividing (3-7) into \(S\Delta{t}\) we get

\(p {~=~} \frac{\Large\overline{F}}{S} {~=~} \frac{1}{3} mn \overline\upsilon^2 \)(3-8)

This is the basic equation of molecular-kinetic theory of gases.
The pressure of gas is proportional to the product of the mass of the molecule, the number of molecules per unit volume and the average square of the motion speed of gas molecules.

If through \( \large\overline{E} \) denote the average kinetic energy of the translational motion of the molecule

\(\overline{E} {~=~} \frac{m\overline{\upsilon}^2}{2} \)

then equation \((3-8)\) can be written in the form of

\(p {~=~} \frac{2}{3} n\overline{E} \)

In conclusion, even though the calculation is done without obvious molecular collisions, it does not mean that the collisions are not considered at all. It is the huge number of collisions that leads to the fact that the movement of molecules is completely chaotic. The equations \((3-2), (3-4)\) and \((3-6)\) are performed with great accuracy precisely because of the huge number of collisions. At normal atmospheric pressure, for example, the molecule experiences about a billion collisions per second.