140. Magnetic field energy

Let's find energy, which has an electric current \(I\) in the conductor. According to the law of energy conservation, it is obvious that the energy of current is equal to the work, or the energy that the power source has to spend in order to create the electric current. When the current stops, this energy is released in one form or another.

When closing a circuit containing a constant EMF (ElectroMotive Force), the power of source EMF is initially used to generate electrical current, i.e. to drive the conductor electrons, and partly to generate heat. Once the constant current force value is set, the entire power of source EMF will be used exclusively to generate heat. The energy of the current does not change anymore. Simply by means of current, the chemical energy of the battery is converted into heat.

In the same way, in order to accelerate a car on a horizontal section of the track to a constant speed \(\upsilon\), the work \(m\upsilon^2/2\) must be done. Part of the engine's power is used to overcome friction and part is used to increase car speed.

At \(\upsilon=const\), all engine power is used to overcome friction, and the kinetic energy of the car does not change.

Now let's find out why it is necessary to do the work to create electric current. The point is that when the circuit is closed, when the current starts to increase, there is appeared EMF self-induction \(\Large\varepsilon\small{_i}\) directed against the EMF of the current source. In order for the current to reach its final value \(I\), the battery must perform work against the vortex (eddy) field forces. This is the work that goes into increasing the energy of electric current. The current force in the circuit, as we already know, is not immediately set. It increases until all the energy consumed by the source in a unit of time begins to release heat in it.

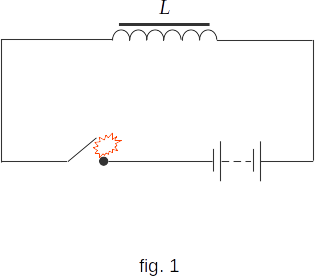
On the contrary, when the circuit breaks and the current disappears, the stored energy \((\frac{1}{2}LI^2)\) is released. A spark is formed, quite powerful if the inductance of the circuit is high (fig. 1). The appearance of the spark is caused by the EMF self-induction, which will now be positive, as the vortex field is directed along the current at opening.

To determine the energy of current it is necessary to calculate the work done by the EMF source to create current. The calculations are quite complex, and we won't be doing them. To find an equation for the energy of current flowing through the circuit with inductance \(L\), we can use the analogy between inertia and self-induction, which was mentioned in \(\S 138.\)

If self-induction is similar to inertia, then inductance \(L\) in the process of generating current must play the same role as mass \(m\) when the body speed increases in mechanics. The role of body speed \(\upsilon\) in electrodynamics is played by current force \(I\) as a value that characterizes the movement of electric charges.

If it's so, then the energy of current \(U_m\) (energy stored) can be considered as a value similar to the kinetic energy of the body in mechanics \(\frac{1}{2}m\upsilon^2\), and be written as

\( U_m \,= \,\frac{1}{2}LI^2 \) (12-7)

It is the equation for energy of current that results from the calculations.

Energy of a current \((12-7)\) is expressed not through the values characterizing a magnetic field, but through the geometrical characteristic of conductor \(L\) and current force \(I\) in it. But the same energy can be expressed through the characteristics of the magnetic field. Calculations show that the density of energy of the magnetic field (i.e. energy of a volume unit) is proportional to the square of the magnetic induction, just as the density of energy of the electric field is proportional to the square of the electric field strength

\( \eta_b \,= \,\frac{energy}{volume} \,= \,\frac{1}{2}\frac{B^2}{\mu\mu_0} \) (12-8)

If we take into account that the density of energy of the electric field is an equation \((8-34),\) we can write the equation for the density full energy of the electromagnetic field as a sum

\( \eta \,= \,\eta_e + \eta_b \,= \,\frac{1}{2}(\varepsilon{_0}\varepsilon\,E^{2} + \frac{B^2}{\mu\mu_0}) \)

This equation for density of energy is valid in all cases.