131. Magnetic flux

In order to give an exact quantitative formulation of Faraday's electromagnetic induction law, it is necessary to introduce a new value - magnetic flux.

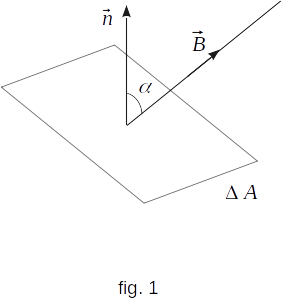
Let's highlight a small area \(\Delta{A}\) in the magnetic field. The area should be so small that the magnetic induction in all points of the area can be considered the same. Let \(\overrightarrow{n}\) be normal to the area \(\Delta{A}\), forming an angle \(\alpha\) with the direction of the magnetic induction vector \(\overrightarrow{B}\) (fig. 1). The magnetic flux \(\Delta{\Phi_B}\) through the area \(\Delta{A}\) is the value equal to the projection of the magnetic induction vector to the normal to the area multiplied by the area size

\( \Delta{\Phi_B} \,= \,B_n\,\Delta{A} \,= \,B\,\Delta{A}\,cos\alpha \)

The flux can be either positive or negative depending on the size of the angle.

If the magnetic field is homogeneous, the flux through a flat surface with dimensions \(A\) is equal to

\( \Phi_B \,= \,B\,A\,cos\alpha \) (12-1)

The magnetic flux can be visually represented as a value proportional to the number of vector \(\overrightarrow{B}\) lines penetrating this area.