136. Electromotive force induction in moving conductors

If the conductor moves in a magnetic field that is constant in time, the EMF induction in the conductor will not come from a vortex electric field (this field simply does not exist), but from another cause.

When a conductor moves, its free charges move with it. Therefore, the Lorentz force will act on the charges from the magnetic field. That's what causes the charges to move inside the conductor. EMF induction therefore has "magnetic origin".

In many power plants it is the Lorentz force that causes the electrons to move in moving conductors.

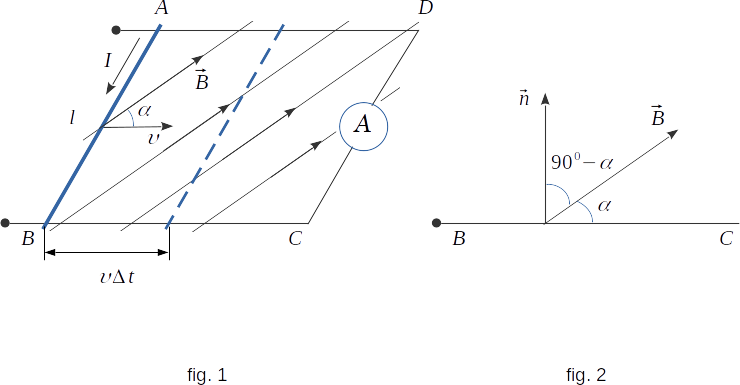
Let's calculate the EMF induction for a rectangular circuit placed in a homogeneous magnetic field (fig. 1). Let the \(AB=l\) side of the loop move at a constant velocity \(\overrightarrow{\upsilon}\) along the \(BC\) and \(AD\) sides, remaining parallel to the \(CD\) side all the time. The electrical circuit will be closed and the inductive current can be detected by a galvanometer. The induction vector \(\overrightarrow{B}\) of homogeneous magnetic field is perpendicular to the conductor \(AB\) and sets angle \(\alpha\) with the direction of its velocity.

The force, which acts on the charged particle from the magnetic field side (see \(\S{128}\)), is equal in modulus

\( F_m \,= \,|q_0|\,\upsilon\,B\,sin{\alpha} \) (12-3)

This force is directed along conductor \(AB\). The work of the Lorentz force to move a single charge along the conductor at distance \(l\) is equal to

\( W \,= \,F_m\,l \,= \,|q_0|\,\upsilon\,B\,l\,sin{\alpha} \)

Electromotive force induction in conductor \(AB\) is equal to the ratio of Work for moving a single charge \(q_0\) to this Charge

\( \Large{\varepsilon}\small{_i} \,= \,\frac{W}{q_0} \,= \,\upsilon\,B\,l\,sin{\alpha} \) (12-4)

This equation is true for any conductor with length \(l\) moving at a speed of \(\overrightarrow{\upsilon}\) in a homogeneous magnetic field.

In other conductors of the circuit EMF is equal to zero because the conductors are fixed. Consequently, EMF in the entire \(ABCD\) circuit is equal to \(\Large{\varepsilon}\small{_i}\) and remains constant if the velocity \(\overrightarrow\upsilon\) is constant. The electric current will increase as the displacement of the \(AB\) conductor to the right decreases the total resistance of the circuit.

On the other hand, EMF induction can be calculated using the electromagnetic induction law \((12-2)\). In fact, the magnetic flux through the \(ABCD\) circuit is

\( \Phi_B \,= \,B\,A\,cos{(90^0 - \alpha)} \,= \,B\,A\,sin{\alpha} \)

Where the angle \((90^0 - \alpha)\) is the angle between vector \(\overrightarrow{B}\) and normal \(\overrightarrow{n}\) to the loop surface (fig. 2), and \(A\) is the \(ABCD\,\) loop area. If we assume that at the initial moment \(t=0\) the conductor \(AB\) was at a distance \(BC\) from the conductor \(CD\), when the conductor is moved, loop area \(A\) changes as follows

\( A \,= \,|AB|(|BC| - \upsilon{t}) \)

In time \(\Delta{t}\), the area of the circuit changes by \(\Delta{A}=-l\,\upsilon\,{\Delta{t}}\). A "minus" sign indicates that it's decreasing. The change in magnetic flux during this time is \(\Delta(\Phi)=-B\,l\,\upsilon\,\Delta{t}\,sin{\alpha}\). Consequently,

\( \Large{\varepsilon}\small{_i} \,= \,\frac{\Delta{\Phi}}{\Delta{t}} \,= \,\upsilon\,B\,l\,sin{\alpha} \)

as it was obtained above (see equation \((12-4)\)).

Obviously, if the whole \(ABCD\) loop moves in a homogeneous magnetic field, keeping its orientation with respect to vector \(\overrightarrow{B}\), then the EMF induction in the loop is equal to zero, because the flux \(\Phi\) through the area bounded by the loop does not change. It can be explained in this way. When the loop moves, forces \((12-3)\), which occur in the \(AB\) and \(CD\) conductors, acting on charges from point \(A\) to point \(B\) and from point \(C\) to point \(D\). The total work of these forces when passing the circuit in a clockwise or counterclockwise direction is equal to zero.