60. Molecular picture of thermal expansion

The dependence of the potential energy of interaction of molecules on the distance between them allows to explain the reason of thermal expansion. As can be seen from Figure 1, the curve of potential energy is strongly asymmetric. It rises very quickly from the minimum value at the point \(r_0\) with decreasing \(r\) and grows quite slowly with increasing \(r\).

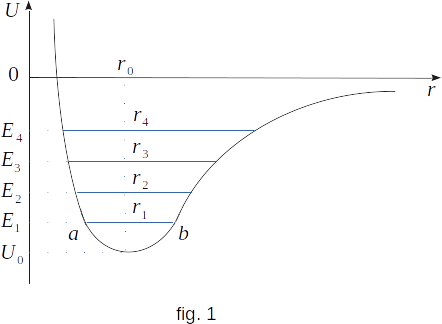
At absolute zero in the equilibrium state the molecules would be at a distance of \(r_0\) from each other, corresponding to the minimum value of potential energy \(U_0\). As the molecule heats up, it starts to vibrate near the equilibrium positions. The range of vibrations is determined by the average energy \(E\). If the potential curve was symmetric, then the average position of the molecule would still correspond to the distance \(r_0\). This would mean that the average distance between the molecules would remain the same during heating and, consequently, no thermal expansion. In fact, the curve is asymmetrical. Therefore, at energy \(E_1\) the average position of an oscillating molecule corresponds to distance \(r_1 > r_0 ~(ar_1 > r{_1}b)\).

Changing the average distance between two neighboring molecules means changing the distance between all molecules of the body. This is why the size of the body increases.

Further heating the body leads to increase the full energy of the molecule up to some value \(E_2\). In this case the average distance between the molecules also increases, because now the oscillations are performed with greater amplitude around the new equilibrium position, \(r_2 > r_1, ~r_3 > r_2\) and so on.

So, we see that when the body heats up, the average distance between oscillating molecules increases, so the size of the body also increases. If we know the shape of the potential curve, we can calculate the coefficient of linear expansion. Calculations of this kind are in good agreement with the experiment.