58. Thermal linear expansion

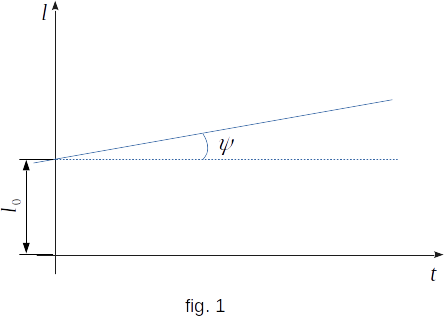
The experiment shows that in case of small temperature changes, the change in linear dimensions of a solid body is proportional to the temperature increase (fig. 1). As lengthening at heating (or shortening at cooling) depends also on initial length of a body, it is more convenient to consider not lengthening of a body itself, but so-called relative lengthening, the ratio of increase in length \(\Delta{l} = l - l_0\) to initial length \(l_0\). The relative lengthening of \(\Delta{l}/l_0\) is proportional to the temperature change \(\Delta{t} = t - t_0\).

\( \frac{\Delta{l}}{l_0} ~= ~\alpha{\Delta{t}} \) (7-1)

The proportionality coefficient \(\alpha\) is called the linear expansion coefficient. It shows, on what fraction of the initial size increases length of a body at heating it on \(1^0{С}\). The coefficient of linear expansion depends on the nature of the substance as well as its temperature. However, if to consider changes of temperature in not too wide limits, it is possible to neglect dependence \(\alpha\) on temperature and to consider factor of linear expansion as a constant for the given substance.

The body length itself depends on temperature changes as follows

\( l ~= ~l_0(1 ~+ ~\alpha{\Delta{t}}) \)

For most substances, the \(\alpha\) value is \(10^{-5} - 10^{-6} deg^{-1}\). The linear thermal expansion of the bodies is very small.