53. Capillary phenomena

The curved surface of the fluid is easiest to observe in thin tubes - capillaries. This is caused by wetting and non-wetting phenomena. The fact is that if the forces of attraction between the molecules of liquid and gas can be neglected, then the attraction between the molecules of liquid and molecules of solid body tube can not be neglected. Therefore, the shape of the surface of the liquid that is in contact with the solid body will depend on whether the forces of attraction between the molecules of liquid and solid are greater or between the molecules of liquid.

In the first case, the liquid will be wetting and its shape at the wall of the capillary is such (Fig. 1), that the angle \(\Theta\) between the surface of the liquid and the wall is sharp. (Liquid sticking to the wall.) In the second case, the liquid does not wet the solid surface and the angle \(\Theta\) is blunt between the surface of the liquid and the wall (Fig. 2 - the liquid pull off the wall).

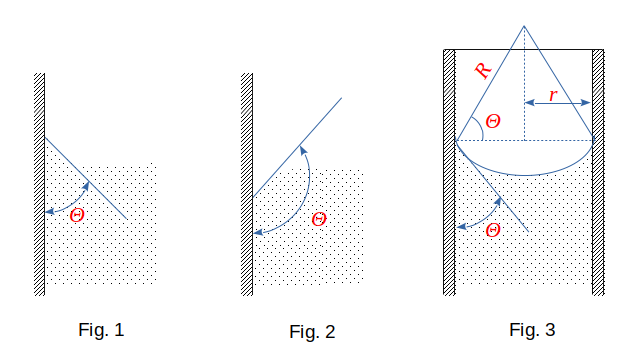
Lets study cases of total wetting (angle \(\Theta ~= ~0^0 \)) and total non-wetting (angle \(\Theta ~= ~180^0 \)).
In thin tubes, the curved surface of the liquid can be assumed to be a hemisphere, the radius of which \(R\) is the radius of the tube's channel \(r\) when fully wetted or not wetted. (In case of incomplete wetting (or non-wetting), the curved surface of the liquid in thin tubes is also taken as part of the surface of a sphere, the radius of which \(R\) is associated with the radius of the tube \(r\) with a ratio \(r ~= R\cos\Theta\) (Fig. 3).)
Right above the surface of the liquid the pressure (equal to atmospheric pressure) is higher than inside the liquid by the value of overpressure (5-5)

\( p_s ~= \frac{2\sigma}{R} \)

Therefore, the liquid in the capillary and in the wide container (Fig. 4) cannot be at the same level. In a capillary with liquid wetting the walls, it must rise to such a height \(h\) that the pressure \(p_b\) at point \(B\) at the base of the capillary and the pressure \(p_c\) at the same level at point \(C\) in a wide container are the same. But,

\( p_c ~= ~p_b ~= ~p_a\)

where \(p_a\) is atmospheric pressure and pressure \(p_b\) can be written as

\( p_b ~= ~p_a + \rho{gh} - \frac{2\sigma}{R} \)

(here \(\rho{gh}\) is the pressure of the liquid column with height \(h\)). Considering that \(~p_a = p_b \), it is possible to find the height of liquid rise in the capillary

\( h ~= ~\frac{2\sigma}{\rho{gR}} \) (5-6)

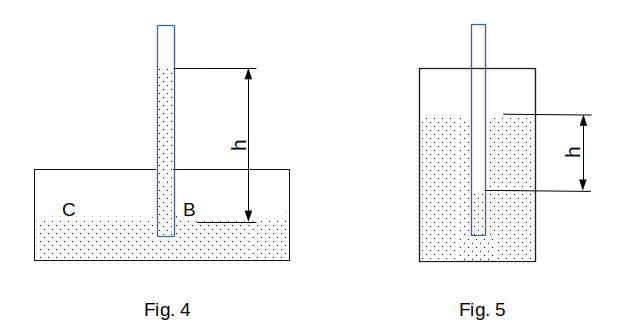
The non-wetting liquid in the capillary, on the contrary, drops to a depth of \(h\) (Fig. 5), because in this case the pressure in the liquid is greater by \(\frac{2\sigma}{R}\) than the pressure above the horizontal surface of the liquid.

Bodies penetrated by a large number of thin channels (capillaries) actively absorb water and other liquids. It is only necessary that the liquids wet the body surface. This is why the towel absorbs water. Rising the water through the capillary fibres of plants plays a very important role in their lives.