51. The force of surface tension

Let's find the magnitude and direction of the surface tension forces. The easiest way to do this is to use a rectangular wire frame, one side of which length \(l\) can move horizontally with low friction (Fig. 1). By dipping the frame in soapy water, it is easy to get a soapy film stretched on the frame. Immediately after that, you can see the crossbar move. The soapy film will shrink its surface. This means that forces perpendicular to the bar are acting on the bar in the direction of the soap film. These are the forces of surface tension. They can be easily measured by applying a force \(F_1\) to the crossbar that would keep the crossbar in equilibrium.

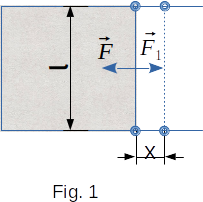
When the bar is moved on the section \(x\), the surface tension force \(F\) will perform the work

\( W ~= 2F_x \)

Multiplier \(2\) appears because the soap film has two surfaces and force \(F\) is applied along each surface.
According to the law of energy conservation, this work is equal to a change in potential (surface in this case) energy taken with the opposite sign

\( W ~= -\Delta(U_s) ~= -(2A_2\sigma - 2A_1\sigma) ~= ~2\sigma(A_1-A_2)\)

where \(A_1\) and \(A_2\) are the starting and ending areas of the soap film.
Obviously,

\( l_x ~= ~A_1-A_2\)

and hence,

\( W ~= ~2F_x ~= ~2\sigma{l_x} \)

From here, the surface tension force acting on a line of length (l_x) at the border of one of the surfaces is equal to

\( F ~= ~\sigma{l_x} \) (5-1)

The force of surface tension is directed tangentially to the body surface and perpendicular to the line limiting this surface (perpendicular to the bar in our case). The force is proportional to the length, and the coefficient of proportionality is the coefficient of surface tension. According to the equation \((5-1)\), the surface tension coefficient \(\sigma\) is measured in newtons per meter (in SI).

This experiment makes it possible to measure the surface tension coefficient. To do this you need to know the length of the bar \(l\) and the force \(F_1\) that keeps the bar in equilibrium.

The table shows the surface tension coefficients for liquids on their border with air.

Liquids	The surface tension coefficient \(N/m\)
Water at \(20^0 C\)	\(7.3 \times 10^{-2} \)
Soap water at \(20^0 C\)	\(4.0 \times 10^{-2} \)
Ethyl alcohol at \(20^0 C\)	\(2.2 \times 10^{-2} \)
Mercury at \(20^0 C\)	\(4.7 \times 10^{-1} \)
Gold at \(1130^0 C\)	\(1.1\)